🎶 차원 축소에 대해 알아보자!
저번 포스트에서는 RNN의 종류 중 하나인 LSTM과 GRU에 대해 알아봤다.
LSTM과 GRU - 장기 의존성 문제를 해결한 RNN
LSTM과 GRU - 장기 의존성 문제를 해결한 RNN
🎶 LSTM과 GRU에 대해 알아보자! 지난 포스트에서는 RNN 중 가장 간단한 구조를 갖고 있는 vanilla RNN에 대해 알아봤다.RNN(Recurrent Neural Networks)이란? RNN(Recurrent Neural Networks)이란?🎶 RNN에 대해 알아보
ybbbb.tistory.com
이번 포스트에서는 '차원 축소'에 대해 다뤄보도록 하겠다.
차원(dimension)이란,
어떤 공간에 존재하는 데이터들을 식별하는 데에 필요한 최수 수의 좌표값을 뜻하는데, 예를 들어 2차원 공간의 점들은 2개의 값을 가진 좌표로 표현하고, 3차원 공간의 점들은 3개의 값을 가진 좌표료 표현할 수 있다.
즉, 차원은 데이터를 다룰 때 각 데이터를 표현하는 특징(feature)의 수라고도 할 수 있는데, 데이터가 많은 수의 특징으로 표현된다면 차원도 같이 증가하게 되는 것이다.
여기서 바로 차원 축소의 필요성이 대두되게 되는데, 높은 차원의 데이터는 많은 양의 데이터를 가지고 있지만, 이 데이터 가운데 상당한 부분은 중요하지 않은 내용일 가능성이 높다. 이에 높은 차원의 데이터를 다룰 때는 중요하지 않은 차원을 생략하고 중요한 차원만 남기는 '차원 축소(dimensionality reduction)'가 필요해진 것이다!
차원 축소에서 가장 중요한 것은 차원을 줄일 때 정보의 손실을 최소로 하면서 특징의 수를 줄이는 것으로써, 이는 '차원의 저주(curse of dimensionality)'를 피하기 위해 필수적으로 수반돼야 하는 것이다.
(🎃차원의 저주란, 데이터를 다루기 위한 차원이 높아지면 데이터들 사이의 거리가 멀어져서, 공간 내 데이터의 밀도가 낮아지게 되어 데이터들 사이의 관계를 파악하는 것이 힘들어지는 것을 말한다.)
그렇다면 차원 축소를 위한 분석 기법에는 어떤 것들이 있을까?
바로 가장 일반적이면서 효과적인 방법이 '주성분 분석(principal component analysis) 이하 PCA'이다.
데이터의 분산을 가장 잘 유지하는 축들을 주성분이라고 하는데, 여러 축으로 구성된 주성분들 중 첫 번째 주성분은 데이터의 분산을 가장 잘 표현하는 방향벡터이고, 두 번째 주성분은 첫 번째 주성분과 직교하는 축들 가운데 데이터의 분산을 가장 잘 보존하는 방향벡터이다.
즉, k번째 주성분은 이전의 k-1개의 주성분과 모두 직교하면서 데이터의 분산을 가장 잘 보존하는 축이라고 정의할 수 있다!
⚔️ 정리하자면, 주성분 분석은 데이터의 특징을 잘 보존하는 투영면을 찾기 위해 분산을 가장 잘 유지하는 축을 찾아, 이들을 이용하여 투영면을 구성하는 것이다!
이 주성분 축들을 찾는 방법은,
- 분산을 최대로 유지하는 축을 찾기
- 찾은 축에 직교하면서 남은 분산을 최대로 유지하는 축 찾기
- 원하는 투영면의 차원에 도달할 때까지 2번을 반복
으로 총 3단계를 거치고, 여기서 찾은 순서에 따라 i번째 주성분이라고 부른다.
수식으로 표현하면 다음과 같은데,

n차원 데이터 m개를 mxn 행렬로 표현한 M 행렬이 있다고 할 때, 이 행렬의 '공분산(covariance)행렬'인 C를
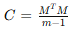
위와 같이 구해 '고유값 분해(eigenvalue decomposition)'를 실시한다. 분해를 통해 공분산 행렬은 '고유벡터(eigenvector)'로 이루어진 행렬 W와 고유값을 가진 대각행렬 Λ로 분해되는데, 이때 W를 구성하는 기저 벡터 이하 각 열 벡터들이 바로 주성분인 것이다.
즉, M개의 분산을 최대로 보존하면서 k차원으로 축소시킨 M(k)를 얻는 방법은 주성분들 중 중요한 k개의 주성분을 기저로 하는 공간으로 옮기면 되는데, 그 방법은 다음 수식과 같이

W의 k개 열만을 추출한 W(k)를 이용하여 구한다.
마지막으로, 예를 통해 위 과정을 이해하도록 해보자.
우선, 임의의 2차원 데이터를 다음과 같이 선택했다고 가정하자.
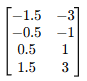
위 데이터의 공분산 행렬을 수식을 통해 구하면 다음과 같고,

이 공분산 행렬을 '고유값 분해'를 통해 다음과 같이 고유값과 고유벡터를 구할 수 있고,
(🎃고유값 분해에 대해서는 다음 위키백과에 잘 설명돼 있으므로, URL만 첨부하도록 하겠다.)
고유값 분해 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org

고유값이 가장 큰 첫 번째 고유벡터를 첫 번째 주성분으로 선택한 후, 이 방향으로 데이터를 투영하면, 다음과 같이 1차원으로 축소된 데이터 Z를 얻을 수 있다.
(🎃주성분의 순서는 고유값이 큰 값부터 차례대로 선택해야 원래 데이터의 분산을 가장 잘 보존하는 축 순서대로 주성분을 선택할 수 있게 된다.)

⚔️ 정리하자면, 데이터의 차원 내지는 특성의 값이 매우 클 경우 발생하는 차원의 저주를 피하기 위해 차원 축소를 진행해야 하고, 일반적으로 이 과정은 PCA를 통해 이루어진다.
'머신러닝' 카테고리의 다른 글
| [RL] 강화학습(Reinforcement Learning) - 에이전트, 정책, 정책탐색, 환경, 리턴, 할인율 (2) | 2025.01.16 |
|---|---|
| [RL] 강화학습 알고리즘 - PPO (Proximal Policy Optimization) with TRPO, Clipped Surrogate Objective, GAE, 상태가치함수, 엔트로피 보너스 (2) | 2025.01.15 |
| SVM(Support Vector Machine) - 소프트 마진과 하드 마진, 그리고 커널 트릭 + python 구현까지! (0) | 2025.01.07 |
| K-means clustering 에 대해 알아보고 python 으로 구현해보자! (0) | 2025.01.05 |
| LSTM과 GRU - 장기 의존성 문제를 해결한 RNN (2) | 2024.12.31 |
| RNN(Recurrent Neural Networks)이란? (0) | 2024.12.30 |
| CNN구현 in python - MNIST 데이터셋을 활용하자! (0) | 2024.12.29 |
| CNN(합성곱신경망)이란? (2) | 2024.12.28 |



