🎶 강화학습을 위한 알고리즘 중 하나인 마르코프 결정 과정에 대해 알아보자.
1. 마르코프 결정 과정
1950년대 리처드 벨만(Richard Bellman)이 논문으로 처음 기술한 이 과정은 마르코프 연쇄를 활용한 알고리즘으로, 각 스텝에서 에이전트는 여러 가능한 행동 중 하나를 선택할 수 있고, 전이 확률은 선택된 행동에 따라 달라진다. 특정 상태 전이는 보상을 반환하는데, 에이전트의 목적이 바로 이 보상을 시간이 지남에 따라 최대화하기 위한 정책을 찾는 것이다.

위 그래프를 예로 살펴보자. '상태 S0'에서 시작하면 에이전트는 행동 a0, a1중에 하나를 선택할 수 있는데, a0를 선택하면 50%의 확률로 '상태 S0'으로, 또는 50%의 확률로 '상태 S2'로 상태 전이가 일어나고, a1을 선택하면 100% 확률로 '상태 S2'로 상태 전이가일어나게 된다.
주목할 만한 점은 상태 S1에서 행동 a0을 취했을 때 70% 확률로 S0로 상태 전이가 일어나면서 보상 +5를 받는다는 사실과, 상태 S2에서 행동 a1을 취했을 때 30%의 확률로 S0로 상태 전이가 일어나면서 보상 -1를 받는다는 사실이다.
2. 벨만 최적 방정식과 Q-가치 반복 알고리즘
우리가 원하는 목표는 바로 이 보상을 최대화하는 것이 목적인데, 벨만은 에이전트가 최적으로 행동하면 '벨만 최적 방정식(Bellman optimality equation)'이 적용된다는 사실을 입증했다. 벨만 최적 방정식은 다음과 같이 구성된다.

- P(S' | S, a) : 에이전트가 상태 S에서 행동 a를 선택했을 때 상태 S'로 전이할 확률
- R(S, a) : 에이전트가 상태 S에서 행동 a를 선택했을 때 받을 수 있는 보상
- r : 할인 계수(할인율), 0과 1사이의 값을 가짐
위의 벨만 최적 방정식은 에이전트가 최적의 정책을 따를 때 기대되는 누적 보상의 값으로, 결국 가치 반복 알고리즘에서 쓰이는 상태-행동 쌍의 가치 방정식인 Q-가치 반복 알고리즘과 다음 관계를 갖는다.
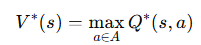
Q-가치 반복 알고리즘은 벨만이 발견한 알고리즘 중 하나로, 에이전트가 상태 S에 도달해서 행동 a를 선택한 후 이 행동의 결과를 얻기 전에 평균적으로 기대할 수 있는 할인된 미래 보상의 합을 의미한다.

결국 에이전트가 취해야 할 최적의 정책은 다음과 같음을 쉽게 확인해 볼 수 있다.

⚔️ 결국 간단히 정리하자면 다음과 같다.
- Q(s, a) 는 상태-행동 쌍의 가치
- V(s) 는 해당 상태에서 최적 행동을 했을 때의 기대 가치
- V(s) 는 Q(s, a) 중 가장 좋은 행동을 선택한 값
3. Python 구현
이 알고리즘을 간단하게 Python으로 구현해보도록 하겠다. 우선 MDP를 파이썬의 행렬로 정의내리자
(🎃 MDP는 사진1과 같은 그래프를 의미한다.)
# 상태 S 에서 S' 으로 상태 전이할 확률
transition_prob = [
[[0.5, 0.0, 0.5], [0.0, 0.0, 1.0]],
[[0.7, 0.1, 0.2], [0.0, 0.95, 0.05]],
[[0.4, 0.0, 0.6], [0.3, 0.3, 0.4]]
]
# 상태 S 에서 S' 으로 상태 전이할 때 받는 보상
rewards = [
[[0,0,0], [0,0,0]],
[[+5,0,0], [0,0,0]],
[[0,0,0], [-1,0,0]]
]
# 각 상태에서 가능한 행동집합
possible_act = [[0,1], [0,1], [0,1]]위의 코드는 사진1의 그래프를 참고해서 작성했는데, 예로 상태 S2에서 행동 a1을 취한 후 S0으로 전이할 확률은 transition_prob[2][1][0], 보상은 rewards[2][1][0] 이다.
이제 Q-가치를 모두 0으로 초기화하자.
import numpy as np
Q_values = np.full((3,2), -np.inf)
for state, actions in enumerate(possible_act):
Q_values[state, actions] = 0.0 # 가능한 모든 행동에 대해서 0으로 초기화
이제 Q-가치 반복 알고리즘을 작성 및 실행해보자.
gamma = 0.9 # 할인계수
for iter in range(50): # 50 번 수행
Q_prev = Q_values.copy()
for s in range(3):
for a in possible_act[s]: # Q-가치 반복 방정식
Q_values[s, a] = np.sum([
transition_prob[s][a][sp] * (rewards[s][a][sp] + gamma * Q_prev[sp].max())
for sp in range(3)])
Q-가치를 확인해 보면, 다음과 같다.

예를 들어 에이전트가 상태 s0에서 행동 a1을 선택했을 때 할인된 미래 보상의 기대 합은 약 3.76인 것이다.
이 Q-가치를 활용해 각 상태에서 에이전트가 취해야 할 행동의 값들은 다음과 같이 구할 수 있다.

즉, 할인계수 0.9를 사용했을 때 각 상태 s0, s1, s2에서 선택할 최적의 행동은 a1, a0 ,a1인 것이다.
'머신러닝' 카테고리의 다른 글
| 오토인코더, GAN(생성적 적대 신경망), 확산 모델의 개념 (0) | 2025.04.24 |
|---|---|
| [RL] 강화학습 - 심층 Q-러닝 알고리즘의 여러 가지 변형 (0) | 2025.04.20 |
| [RL] 강화학습 - 근사 Q-러닝과 심층 Q-러닝 개념 및 Python 구현 (0) | 2025.04.18 |
| [RL] 강화학습 - Q-러닝 개념, 수식 및 Python 구현, 그리고 입실론-그리디 정책 (2) | 2025.04.14 |
| OpenAI Gym - OpenAI Gym 개념과 cartPole-v1, 그리고 정책 하드코딩 (0) | 2025.04.06 |
| 앙상블(Ensemble) - 배깅(Bagging), 부스팅(Boosting), 스태킹 (0) | 2025.01.30 |
| [RL] 강화학습(Reinforcement Learning) - 에이전트, 정책, 정책탐색, 환경, 리턴, 할인율 (2) | 2025.01.16 |
| [RL] 강화학습 알고리즘 - PPO (Proximal Policy Optimization) with TRPO, Clipped Surrogate Objective, GAE, 상태가치함수, 엔트로피 보너스 (2) | 2025.01.15 |



