선형대수 - 역행렬의 개념과 역행렬을 구하는 방법, 그리고 연립일차방정식 풀기

728x90

🎶 선형대수에 쓰이는 역행렬의 개념에 대해 살펴보고, 이를 구하는 방법과 연립일차방정식을 푸는 데 활용하는 방법에 대해 알아보자.

2.6 역행렬

1. 역행렬이란?

정사각행렬 A와 단위행렬 I에 대해,

를 만족하는 행렬 B가 존재하면 A를 '가역행렬(invertible matrix)' 내지는 정칙행렬(nonsingular matrix)라 한다. 이 때, B를 'A의 역행렬(inverse matrix)'라 하고,

로 표시한다.

참고로, 정사각행렬 A가 가역행렬이면, A의 역행렬은 유일한데, 그 이유는 다음과 같다.

만약 B와 C를 A의 역행렬이라고 하자. 그러면,

Uniqueness_of_inverse_matrix — [사진3] 역행렬의 유일성

에 의해 간단하게 증명된다.

더해서, n차 정사각행렬 A, B에 대해 A와 B가 모두 가역행렬이면, 이들의 곱 AB도 가역행렬이고 다음과 같은 식이 성립한다.

property_of_inverse_matrix — [사진4] 가역행렬의 특징

2. 역행렬 구하기

임의의 n차 정사각행렬 A에 대해, n x 2n 행렬 [ A : I ] 에 기본행연산을 시행해 점선의 좌측에 있는 행렬이 단위행렬이 될 때, 점선의 우측에 나타나는 행렬이 A의 역행렬이다. 만약 기본행연산을 시행해도 점선의 좌측에 있는 행렬이 단위행렬로 바뀌지 않으면, A의 역행렬은 존재하지 않는 것이다.

예로, 다음과 같은 행렬 A를 생각해보자.

이를 [ A : I ] 꼴로 변환시킨 후, 다음과 같이 가우스-조르단 소거법 내지는 기본행연산을 수행하면,

row_opeartion_for_inverse_matrix — [사진6] 가우스-조르단 소거법

다음과 같이 A의 역행렬을 구할 수 있다.

3. 역행렬을 활용해 연립일차방정식 풀기

계수행렬을 A, 상수항을 b라고 하면 연립일차방정식을 Ax = b 꼴로 표현할 수 있다. 여기서,

calculate_equations_using_inverse_matrix — [사진8] 역행렬을 활용한 연립일차방정식 계산

에 의해 다음과 같은 해를 얻을 수 있다.

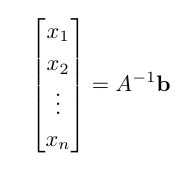
solution_of_equations — [사진9] 연립일차방정식의 해